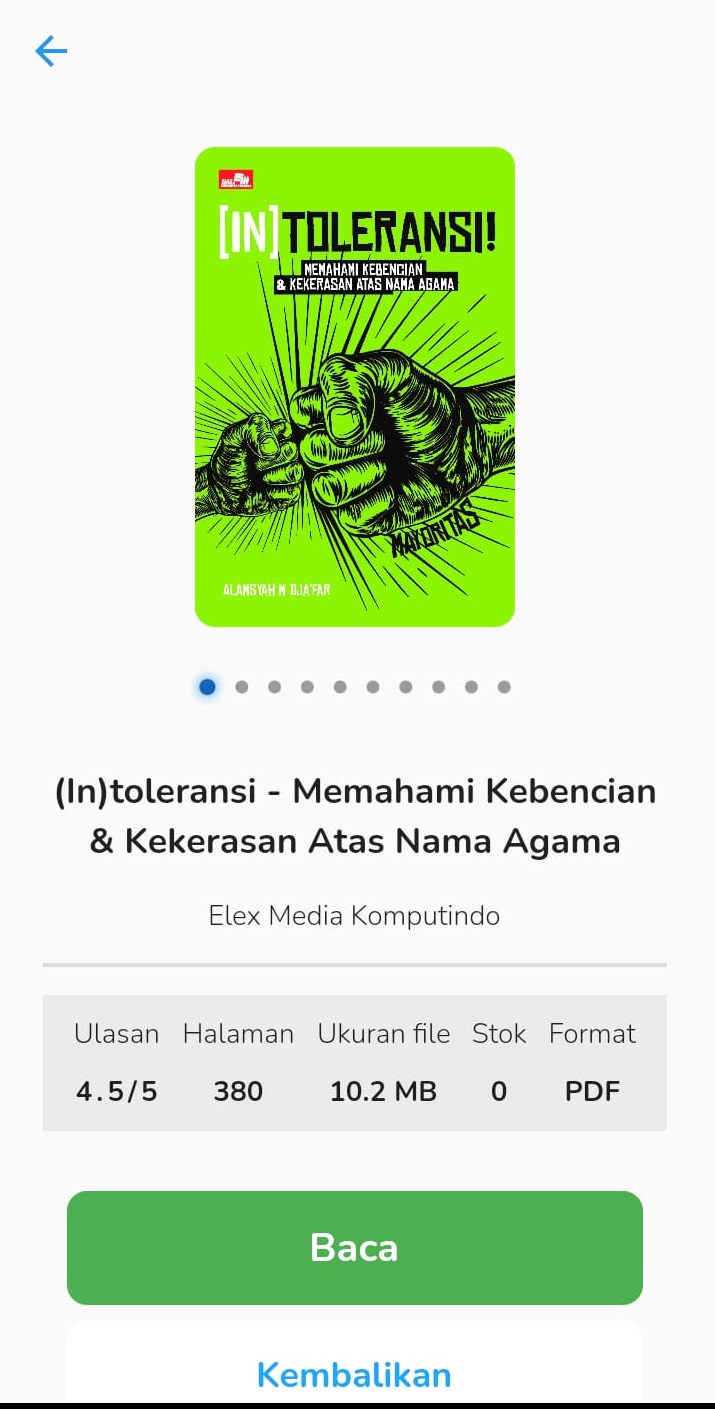
A contamination model for the stochastic order
ÁLVAREZ-ESTEBAN , P. C. - Personal Name

of scenarios. However, it is often a restrictive model, not supported by the data even
in cases in which the researcher tends to believe that a certain variable is somehow
smaller than other. Alternatively, we propose to look at a more flexible version in
which two distributions satisfy an approximate stochastic order relation if they are
slightly contaminated versions of distributions for which stochastic order holds. The
minimal level of contamination required for stochastic order to hold is used as a
measure of deviation from exact stochastic order model. Our approach is based on
the use of trimmings of probabilities. We discuss their connection to approximate
stochastic order and provide theoretical support for its use in data analysis, proving
uniform consistency and giving non-asymptotic bounds for the error probabilities of
our tests. We provide simulation results and a case study for illustration.
| EB00000004453K | Available |
Series Title
-
Call Number
-
Publisher
: ,
Collation
-
Language
ISBN/ISSN
-
Classification
NONE
Content Type
E-Jurnal
Media Type
-
Carrier Type
-
Edition
-
Subject(s)
asymptotics
Bootstrap
Stochastic order
Contamination model
Trimmed distribution
Uniformly consistent test
Specific Detail Info
-
Statement of Responsibility
P. C. Álvarez-Esteban 1...[et al]